Porównanie powierzchni Matrix, Eheim Substrat Pro i JBL MicroMec
Matrix jest produktem firmy Seachem Laboratories produkowanym z naturalnej skały i sprzedawanym jako biologiczny wkład filtracyjny.
Na rynku dostępne są dwa podobne produkty: Substrat Pro firmy Eheim i MicroMec JBL-a.
Prezentujemy porównanie powierzchni filtracyjnej tych wkładów.
Porównanie powierzchni właściwej Matrix, Eheim Substrat Pro i JBL MicroMec
Dr George L. Batten Jr.
Dr Gmerice K. Lafayette
Seachem Laboratories, 1000 Seachem Drive, Madison, GA, USA
Streszczenie
Metoda BET analizy powierzchni ciał stałych wykazała, że powierzchnia właściwa wkładu filtracyjnego Matrix jest 10 razy większa niż Substrat Pro i 20 razy większa w porównaniu z MicroMec. Rozmiar porów Substrat Pro i MicroMec mieści się w zakresie właściwym dla przebiegu procesów biologicznych, podczas gdy w Matrix występują także pory o średnicy pozwalającej na występowanie procesów fizycznych i chemicznych. Ocena geometrii porów wykonana dwiema metodami wskazuje, że aktywna biologicznie powierzchnia w Matrix jest 4 – 4,5 razy większa niż w Substrat Pro i 8 – 9 razy większa niż w MicroMec.
Wstęp
Matrix jest produktem firmy Seachem Laboratories produkowanym z naturalnej skały i sprzedawanym jako biologiczny wkład filtracyjny. Na rynku dostępne są dwa podobne produkty: Substrat Pro firmy Eheim i MicroMec JBL-a. Obydwa wytwarza się ze spiekanego szkła, a producenci utrzymują, że ich powierzchnia właściwa jest większa niż Matrix-a.
W przypadku filtracji biologicznej tak zwana powierzchnia właściwa (mierzona jako pole powierzchni na gram lub pole powierzchni na określoną jednostkę objętości materiału) jest niezwykle ważna, ponieważ to właśnie ona decyduje, ile miejsca będą miały osadzające się na wkładzie filtracyjnym mikroorganizmy. Im jest większa, tym więcej bakterii jest w stanie się na niej rozwinąć. Ważnym elementem jest również wielkość porów. Jeśli mają dużą średnicę (powyżej 10 mikronów), powierzchnia właściwa jest mniejsza. Dążenie do zmniejszania średnicy porów obarczone jest jednak pewnym ryzykiem. Ich zbyt wysoka liczba przy małej średnicy wcale nie oznacza, że produkt, mimo dużej powierzchni właściwej, będzie dobrym biologicznym wkładem filtracyjnym. Zbyt małe pory spowalniają rozwój znajdujących się wewnątrz nich bakterii, hamując przepływ wody dostarczającej składników odżywczych i odprowadzającej produkty przemiany materii. Warto jednak zaznaczyć, że mniejsze pory pełnią ważną rolę w procesach chemicznych i fizycznych, takich jak adsorpcja.
W poniższej pracy autorzy skupili swoją uwagę na ocenie powierzchni właściwej i rozkładzie średnicy porów (która nie będzie jednakowa we wszystkich przypadkach).

Model adsorpcji BET
Izoterma BET jest teoretycznym modelem adsorpcji, który został opracowany w 1938 roku przez Stephena Brunauera, Paula Hugha Emmetta i Edwarda Tellera (Brunauer et al.). Dla osób interesujących się historią nauki, ciekawa może okazać się informacja, że Edward Teller zaledwie cztery lata po opublikowaniu wyżej wspomnianej teorii wziął udział w spotkaniu, które dało początek projektowi Manhattan. W 1943 roku przeprowadził się do Los Alamos, gdzie pracował przy konstrukcji pierwszej bomby atomowej. Często określany jest mianem „ojca bomby wodorowej”.
Teoria BET nie jest wyjątkowo skomplikowana, ale aby docenić jej przydatność w określeniu powierzchni właściwej nie musimy wnikać w jej szczegóły. Według słów jednego z autorów:
„Choć panuje powszechna zgoda, że teoria BET była oparta na uproszczonym modelu adsorpcji wielowarstwowej z fazy gazowej, metoda ta jest używana jako standardowa do oceny powierzchni substancji o dużym stopniu rozdrobnienia oraz porowatych. Istnieją przynajmniej dwa główne powody jej popularności: po pierwsze, w odpowiednich warunkach metoda BET dostarcza w miarę wiarygodnej oceny pojemności monowarstwy – szczególnie, kiedy wykorzystywane są dane adsorpcji azotu w temperaturze 77K; po drugie sama metoda nie jest trudna do zastosowania (Sing).”
Lub, używając bardziej naukowego języka:
„Równie duże znaczenie ma fakt, że w zakresie ciśnień względnych ograniczonych do uzyskania monowarstwy (0,05≤P/P0≤0,3) teoria BET i izotermy uzyskane metodami eksperymentalnymi są zgodne, co czyni metodę BET niezwykle użyteczną w ocenie wielkości powierzchni (Lowell et al.).”
Wszechstronność i dokładność metody BET nie przestaje zadziwiać, choć od jej opracowania minęło 70 lat. W opublikowanych ostatnio pracach wykazano przydatność metody do oceny powierzchni nowego rodzaju porowatych nanomateriałów należących do klasy MOF (Metal Organic Framework), charakteryzujących się ogromną powierzchnią właściwą. Do obliczania jej wielkości stosuje się między innymi metodę BET.
Dwóch badaczy podjęło się tytanicznej pracy porównania danych osiągniętych za pomocą analizy BET z wyliczeniami opartymi o badania budowy krystalicznej. Według ich słów:
„Powierzchnia właściwa BET wyliczona z symulacji izoterm jest porównywalna z polem powierzchni wyliczonym bezpośrednio z oceny geometrycznej struktur krystalicznych. Wyniki te udowadniają, że teoria BET może być wykorzystywana przy obliczaniu pola powierzchni materiałów typu MOF (Walton i Snurr).”
Po przejrzeniu zgromadzonej literatury, autorzy niniejszej pracy są pewni, że metoda BET z wykorzystaniem danych adsorpcji azotu jest wystarczająca do oceny powierzchni właściwej.

Porozymetria rtęciowa
Równanie, które dostarczyło podstaw do opracowania techniki porozymetrii rtęciowej zostało opracowane i udoskonalone w 1805 i 1806 roku (Young, Laplace). Pierwsze urządzenie pomiarowe skonstruowano w 1945 roku (Ritter i Drake). Idea leżąca u podstaw tej metody jest prosta do wyjaśnienia, tak jak proste jest równanie zaproponowane przez Younga i Laplace’a:
D=4γcosθ/P
Gdzie D jest średnicą pojedynczego poru, γ – wartością napięcia powierzchniowego użytej cieczy, cosθ to cosinus granicznego kąta zwilżenia badanego materiału, a P – wartość ciśnienia wywieranego na ciecz. Chcąc obliczyć wartość D, rtęć (której napięcie powierzchniowe γ można znaleźć w źródłach literaturowych lub szybko zmierzyć; podobnie jak graniczny kąt zwilżenia θ, wynoszący najczęściej 130 – 140 stopni), poddaje się działaniu ciśnienia P, w wyniku którego wnika ona w badany materiał, a następnie mierzy się objętość pochłoniętej substancji. Jak widać metoda jest bardzo prosta (wymagane jest tylko przyjęcie pewnych założeń dotyczących kształtu porów). Przy różnych wartościach ciśnienia rtęć jest wtłaczana do porów o różnym rozmiarze, co pozwala uzyskać informację o rozkładzie ich wielkości. Następnym etapem jest wykonanie odpowiednich obliczeń, w oparciu o założenia geometryczne. Niestety, oznacza to, że metoda nie jest idealnie dokładna. W tej prostej procedurze istnieje kilka założeń, a których wiadomo, że nie są prawidłowe. Metoda zakłada na przykład, że kapilary absorbujące rtęć mają taki sam kształt, co jest błędem. Zakłada się też, że materiały podlegające analizie są sztywne, co jest prawdą w przypadku naszych badań, ale na przykład nie podczas analizy tkanin (Nagy i Vas). Kolejnym problemem może być nacisk wywierany na badany materiał. Istnieje ryzyko zniszczenia próbki, jeśli analizie poddawane są na przykład leki (Westermarck).
Mimo swoich niedoskonałości porozymetria rtęciowa jest używana już od wielu dekad. Doskonale sprawdza się przy porównywaniu parametrów podobnych materiałów (błędy pojawiające się podczas analizy jednego będą z dużym prawdopodobieństwem dotyczyły wszystkich i w sumie nie wpłyną na wynik). Dlatego autorzy zdecydowali się na wykorzystanie tej metody do oceny rozkładu porów w trzech rodzajach mediów filtracyjnych. W przypadku szczegółowych obliczeń zostaną użyte współczynniki, co pozwoli na wyeliminowanie błędów.

Eksperyment
Ocena powierzchni właściwej metodą BET i rozkładu średnicy porów zbadany za pomocą porozymetrii rtęciowej zostały wykonane w Micromeritics Analytical Services w Norcross w stanie Georgia.
Analizę BET trzech próbek przeprowadzono w temperaturze 77,3K. Wszystkie próbki były odgazowywane przez 4 godziny w temperaturze 473,15K. Analizę przeprowadzono za pomocą aparatu TriStar 3000 V6.08A.
Dane porozymetryczne uzyskano za pomocą porozymetru rtęciowego AutoPore IV 9500 V1.07. Przyjęto kąt graniczny zwilżenia równy 130 stopni, a wprowadzona wartość napięcia powierzchniowego wynosiła 485 dyn/cm.
Wyniki
Wyniki otrzymane metodą analizy powierzchni BET prezentuje zamieszczona poniżej tabela:
| Próbka | Powierzchnia właściwa BET m2/g | Gęstość pozorna g/dm3 | Powierzchnia właściwa BET m2/dm3 |
| Matrix | 2,1172 | 752 | 1592 |
| Substrat Pro | 0,2171 | 656 | 142 |
| MicroMec | 0,1051 | 888 | 9 |
Gęstość pozorna wyraża stosunek masy suchego materiału do jego objętości, łącznie z porami. Próbki materiałów filtracyjnych umieszczono w cylindrach miarowych o objętości 500ml i zważono na wadze laboratoryjnej. Następnie każdy wynik pomnożono przez 2. Wartość ta jest użyteczna dla akwarysty, ponieważ pozwala ocenić powierzchnię właściwą przy odmierzeniu znanej objętości produktu. W tym miejscu warto zaznaczyć, że zmiana jednostek z metrów kwadratowych/gram na metry kwadratowe /dm3(litr) może prowadzić do błędów. Istnieje bowiem kilka rodzajów gęstości, które mogą być wykorzystane. Autorzy zdecydowali się na tę z nich, która jest najbardziej sensowna dla akwarystów. Można też wyliczyć gęstość całkowitą, będącą stosunkiem masy pojedynczego ziarna ze spiekanego szkła podzielonej przez objętość tego ziarna. Wynik będzie wyższy niż w przypadku metody zastosowanej powyżej. Za pomocą porozymetru rtęciowego można wyliczyć gęstość nasypową oraz gęstość szkieletową. Obydwie mają wyższe wartości niż gęstość pozorna. Na przykład dla Substrat Pro Eheima gęstość pozorna wynosiła 656 g/dm3. Wartość gęstości nasypowej otrzymana za pomocą porozymetru wyniosła 1190 g/dm3, a szkieletowa – 2307 g/dm3. Takie wyniki mogłyby być prawidłowe, gdyby Substrat Pro był wytwarzany w formie bloku o objętości jednego litra, bez wolnych przestrzeni między cząstkami, co obniża gęstość rzeczywistą.
Poniższa tabela prezentuje wpływ gęstości na powierzchnię właściwą określoną metodą BET dla Substrat Pro firmy Eheim:
| Gęstość | Powierzchnia właściwa BET m2/dm3 |
| Pozorna | 142 |
| Nasypowa | 258 |
| Szkieletowa | 501 |
Powierzchnia właściwa produktu zamieszczona na opakowaniu jest bliska wartości, wyliczonej przez autorów z użyciem gęstości szkieletowej.
Trudności z określeniem gęstości nie dotyczą wyłącznie produktów przeznaczonych dla akwarystów. Gałęzie przemysłu, gdzie wykorzystuje się materiały sprężyste (guma tkaniny, papier), mają poważne trudności z określeniem ich gęstości. Choć autorzy tej pracy zdecydowali się na metodę, która ich zdaniem jest najodpowiedniejsza, istnieje jednak ryzyko wystąpienia błędów. Jak mocno granulat został ubity w cylindrze? Jakiemu ciśnieniu został poddany?
Wydaje się jasne, że dla hobbystów byłoby wygodniej, gdyby powierzchnię właściwą określano w metrach kwadratowych/gram. Pozwoliłoby to całkowicie uniknąć konieczności pomiaru gęstości. Jednak z przyczyn historycznych różne typy gęstości są stosowane przy przeliczaniu jednostek powierzchni właściwej określonej metodą BET z metrów kwadratowych/gram na metry kwadratowe/decymetr sześcienny. Jak widać z zamieszczonej powyżej tabeli podczas przeliczenia jednostek mogą pojawić się bardzo odmienne wartości liczbowe.
Wykresy zamieszczone poniżej pokazują rozkład średnicy porów uzyskany za pomocą porozymetrii rtęciowej. Na osi y przedstawiono logarytm intruzji cząstkowej w ml/g lub dV/dlogD, gdzie V to objętość rtęci wtłoczonej do porów ziaren w próbce. Jak widać jest to pochodna wtłoczonej objętości rtęci względem logarytmu średnicy poru. Pochodna w odniesieniu do log D jest używana zamiast pochodnej względem D, kiedy chcemy zwiększyć wartości dV/dD dla D większego niż 2 mikrony. Wykres pochodnej ma tę zaletę, że wyraźnie widać na nim punkty przegięcia, co w tym przypadku pokazuje nagromadzenie porów o konkretnej średnicy.
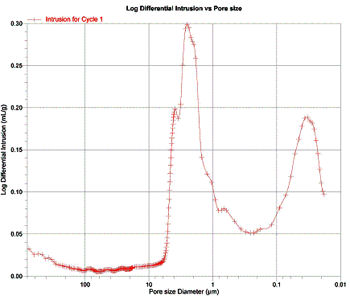
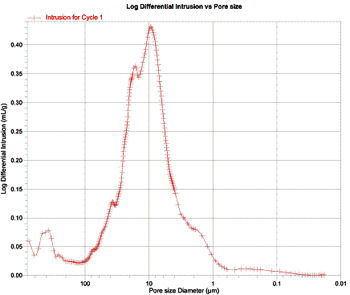
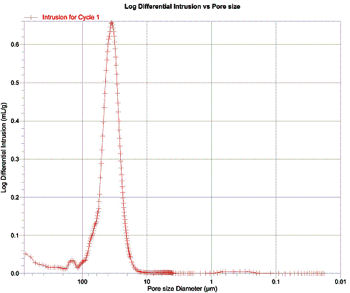
Pierwszą rzeczą, jak rzuca się w oczy podczas analizy wykresów jest to, że jedynie w przypadku wkładu Matrix mamy do czynienia z rozkładem dwuwierzchołkowym. Oznacza to obecność porów o średnicy 1 – 8 mikronów (należy pamiętać, że skala na osi x jest logarytmiczna). Drugi punkt skupienia odpowiada porom o średnicy 0,02 – 0,1 mikrona. Na wykresie dotyczącym Substrat Pro widać pojedynczy, dosyć szeroki wierzchołek odpowiadający zakresowi 4 – 13 mikronów. Biorąc pod uwagę, że skala x jest skalą logarytmiczną, wierzchołek jest w rzeczywistości jeszcze szerszy niż widoczny na wykresie. Z kolei na Wykresie 3 widać pojedynczy, stosunkowo wąski wierzchołek. W rzeczywistości jest on niezwykle szeroki (skala logarytmiczna!), obejmuje bowiem wartości 20 – 60 mikronów.
Otrzymane wyniki są zgodne z tymi uzyskanymi metodą BET dotyczącymi powierzchni właściwej. Wiadomo, że istnieje odwrotna zależność między średnicą porów a powierzchnią właściwą, co obrazują zamieszczone dane. Ziarna wkładu MicroMec charakteryzują się największą średnicą porów i najmniejszą powierzchnią właściwą określoną metodą BET. Matrix ma pory o najmniejszej średnicy, co pokazuje drugi szczyt, a jednocześnie największą powierzchnię właściwą. Substrat Pro plasuje się pośrodku zarówno jeśli chodzi o średnicę porów, jak i powierzchnię właściwą.
Spoglądając na dwuwierzchołkowy Wykres 1 nasuwa się pytanie, jaka część całkowitej powierzchni przypada na pory o średnicy poniżej 0,4 mikrona, które są nieprzydatne z punktu widzenia filtracji biologicznej. Można to wyliczyć zarówno z danych otrzymanych z analizy porozymetrycznej jak i z samego rysunku. Całkowita objętość dla wkładu Matrix uzyskana z danych porozymetrycznych wynosi 0,3331 cm3/g (albo 3,331 x 10-7 m3/g). Ponieważ na wykresie przedstawiono cząstkową objętość w stosunku do średnicy porów, jej całka w odniesieniu do tej wartości (średnicy porów) powinna pozwolić na wyliczenie objętości wtłoczonej rtęci dla każdego fragmentu krzywej. Całkowanie jest łatwe do wykonania, przy założeniu że jego wynik to po prostu obszar pod krzywą. W tej sytuacji zmierzenie powierzchni pod krzywą w przedziale do 0,4 mikrona da pojęcie o tym, jaką część całkowitej powierzchni zajmują pory o średnicy poniżej 0,47 mikrona.
Powiększoną kopię Wykresu 1 skserowano na papierze o gęstości 90 g/m2. Obszar pod krzywą wycięto i zważono otrzymując wynik 0,334 g. Następnie wycięto fragment odpowiadający wielkości porów 0,4 mikrona i mniejszej, który ważył 0,133 g. Oznacza to, że 0,133/0,334 = 0,3982 (39,82%) całkowitej objętości przypada na pory o średnicy 0,4 mikrona i mniejsze.
Aby dowiedzieć się, jaką część całkowitej powierzchni zajmują pory różnych wielkości konieczne jest poczynienie pewnych założeń dotyczących ich kształtu. Aby ustalić granice, można zbadać dwa warianty. Pierwszy zakłada, że wszystkie pory są kuliste. Oznacza to, że pole powierzchni jest proporcjonalne do objętości V podniesionej do potęgi 2/3.
A µ V2/3
W przypadku porów cylindrycznych, pole powierzchni jest proporcjonalne do objętości V podniesionej do potęgi 3/5:
A µ V3/5 dla porów cylindrycznych
Zależność między polem powierzchni a objętością dla porów kulistych jest oczywista, ale w przypadku porów cylindrycznych – już mniej. Poniżej zamieszczono wyjaśnienie obydwu z nich.
Kuli dotyczą poniższe wzory:
V = 4/3pr3,
A = 4pr2
Aby z objętości, gdzie promień podniesiony jest do sześcianu, wyliczyć pole powierzchni, gdzie promień (r) jest podniesiony do kwadratu, należy podnieść objętość do potęgi 2/3, tak więc r3(2/3) = r2.
W przypadku porów cylindrycznych objętość opisuje wzór pr2h, a pole powierzchni 2prh, gdzie h jest wysokością słupa rtęci w cylindrycznej kolumnie. Jednak h jest powiązane z r. Na początku XX wieku dwóch fizyków, pracując niezależnie od siebie nad równaniem Younga Leplace’a, ułożyło i rozwiązało równanie opisujące penetrację cieczy w cylindrycznej kapilarze (Lucas, Washburn). Ich równanie jest powszechnie stosowane (Batten). Dla celów niniejszej pracy wystarczy zaznaczyć, że wzrost wysokości słupa cieczy w kapilarze (h) jest proporcjonalny do pierwiastka kwadratowego z r.
h µ r1/2 dla porów cylindrycznych
Oznacza to, że:
V µ r5/2 i A µ r3/2 więc A µ V3/5 dla porów cylindrycznych
Można teraz ocenić, jaka część powierzchni całkowitej przypada na pory o średnicy 0,4 mikrona i mniejszej. Całkowita objętość wtłaczania wynosi 3,331×10-7 m3/g. Z tego 39,82% objętości (1,326×10-7 m3/g) przypada na pory o średnicy 0,4 mikrona lub mniejszej. Część pola powierzchni przypadająca na małe pory to:
(1,326×10-7)2/3/(3,331×10-7)2/3 = 0,5412 dla porów kulistych;
i
(1,326×10-7)3/5/(3,331×10-7)3/5 = 05755 dla porów cylindrycznych.
Oznacza to, że w przypadku porów kulistych 45,88% pola powierzchni jest użyteczne z punktu widzenia filtracji biologicznej, a w przypadku porów cylindrycznych wartość ta wynosi 42,45%. Mając to na uwadze, można w następujący sposób rozszerzyć Tabelę 1:
| Próbka | Pole powierzchni BET (m2/g) |
| Matrix | 2,1172 |
| Matrix, biologicznie użyteczne kuliste pory | 0,9714 |
| Matrix, biologicznie użyteczne cylindryczne pory | 0,8988 |
| Substrat Pro | 0,2171 |
Z założeń opartych o wyidealizowany kształt porów wynika, że powierzchnia właściwa jest proporcjonalna do objętości podniesionej do potęgi mniejszej od 1. Wzięcie pod uwagę dwóch ekstremalnych wariantów: porów idealnie kulistych i idealnie cylindrycznych doprowadziło do wyliczenia dwóch wykładników o zbliżonej wartości (0,60 i 0,66).
Choć pole powierzchni przypadające na pory zbyt małe, by mogły w nich zachodzić procesy filtracji biologicznej, jest nieco większe niż połowa powierzchni całkowitej, powierzchnia dostępna dla bakterii jest we wkładzie filtracyjnym Matrix i tak większa niż we wkładach Substrat Pro i MicroMec.
Wnioski
Pomiary pola powierzchni metodą BET wskazują, że Matrix ma 10-krotnie większą powierzchnię właściwą niż Substrat Pro i ponad 20-krotnie większą niż MicroMec. Praktycznie cała powierzchnia właściwa w obu tych produktach przypada na pory o większej średnicy, odpowiedniej dla pełnienia funkcji filtra biologicznego, podczas gdy część pola powierzchni ziaren Matrix przypada na drobne pory, w których mogą zachodzić procesy fizyczne i chemiczne (nie biologiczne). Wyniki uzyskane dla dwóch różnych kształtów porów wskazują, że powierzchnia biologicznie aktywna w Matrix jest pomiędzy 4 – 4,5 razy większa niż w Substrat Pro i 8 – 9 razy większa niż w MicroMec.
Literatura
Batten, G. L., in Proceedings of the 1991 International Paper Physics Conference. Atlanta, Georgia: TAPPI Press, 1991 pp. 67 – 70.
Brunauer, S., Emmett, P. H., and Teller, E., J. Am. Chem. Soc. 60: 309 – 319 (1938).
Laplace, P. S. de, Théorie de l’action capillaire, supplément à la traité de mécanique céleste 4o. Paris: 1806.
Lowell, S., Shields, J. E., Thomas, M. A., and Thommes, M., Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density. Dordrecht, South Holland, The Netherlands: Kluwer Academic Publishers, 2004, p. 67.
Lucas, R., Kolloid Zeitschrift 23: 15 (1918).
Nagy, V. and Vas, L. M., Fibres & Textiles in Eastern Europe Vol. 13 No. 3 (51): 21 – 26 (2005).
Ritter, H. L. and Drake, L. C., Ind. Eng. Chem. 17: 782 – 786 (1945).
Sing, K. S. W., in Fraissard, J. P. and Conner, C. W., Eds., Physical Adsorption: Experiment, Theory and Applications. Dordrecht, South Holland, The Netherlands: Kluwer Academic Publishers, 1997, p. 6.
Walton, K. S. and Snurr, R. Q., J. Am. Chem. Soc. 129 (27): 8852 – 8556 (2007).
Washburn, E. W., Phys. Rev. 17 (3): 273 (1921).
Westermarck, S. Use of Mercury Porosimetry and Nitrogen Adsorption in Characterisation of the Pore Structure of Mannitol and Microcrystalline Cellulose Powders, Granules and Tablets. Academic Dissertation. Helsinki, Finland: University of Helsinki (2000).
Young, T., Phil. Trans. Roy. Soc. 95: 65 (1805).

















